小题笔记——求排列中的稳定数个数c/c++

key words：
动态规划
递推算法

题目描述

对自然数1…n，求其全排列中有多少种排列P满足恰好有m个位置Pi>i。

输入数据

共一行，两个正整数n(1≤n≤100)，m(1≤m≤n )。

输出数据

一个整数，满足条件的排列数，需对1e9+7取模后输出

说明

1到5的排列P:5，4，3，2，1有2个位置P1，P2满足Pi>i。

分析：

想办法将题意含有的数字表示出来。

对状态转移方程做一些阐述：

D[n][m]表示从i的全排列中有j个位置满足值大于下标。

那么状态转移方程为：

$D[n][m]=D[n-1][m]*(1+m)+D[n-1]*[m-1](n-m)$

对每一项进行分析：

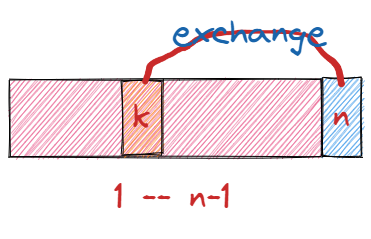
• 第一项：前面n-1项已经满足了有m个稳定数的要求了，那么第n个数可以就放在n位，或者和前面m个稳定数中的任何一个（如k）交换
• 第二项：前面n-1项不满足要求，需要将n与某个非稳定的k交换才可以，而这样的操作能增加一个稳定数，故前面n-1共有m-1个稳定数。k有(n-1-(m-1))种选择。

初始条件：

• m==0的时候只有一种情况，即按顺序。故D[i][0]==1
• m==n-1的时候只有一种情况，即1放在最尾，其它依次前移。故D[i][i-1]==1
• 用循环赋予初值

输出：

D中储存的就是答案了，直接输出即可

Code：

#include<bits/stdc++.h>

using namespace std;

long long D[102][102];

const long long mod=1e9+7;

int main(){

 long long n,m;

 cin>>n>>m;

 for(long long i=1;i<=n;i++){

 D[i][0]=1;//一个稳定数都没有，只有可能顺排

 D[i][i-1]=1;

 //只有一个不是稳定数，只有可能1放在最尾，其他依次往前一个

 }

 for(long long i=1;i<=n;i++)

 for(long long m=1;m<=i-2;m++)//i个数，最多i-1个稳定数，但i-1算了，只需要i-2开始

 D[i][m]=((D[i-1][m]+D[i-1][m]*m)%mod+(D[i-1][m-1]*(i-m))%mod)%mod;

 cout<<D[n][m];

 return 0;

}