小题笔记——走方格c/c++

keyword：
模拟、数学规律

（但是这个题用模拟不对）

题意

从点$(x_1,y_1)$走到$(x_2,y_2)$点(均是整数)，每步能走一个单位长度，只能沿平行于坐标轴的方向运动，每走一步需要向左或向右旋转90°，求最少需要走多少步。
所有坐标满足−10000≤x,y≤10000.

分析

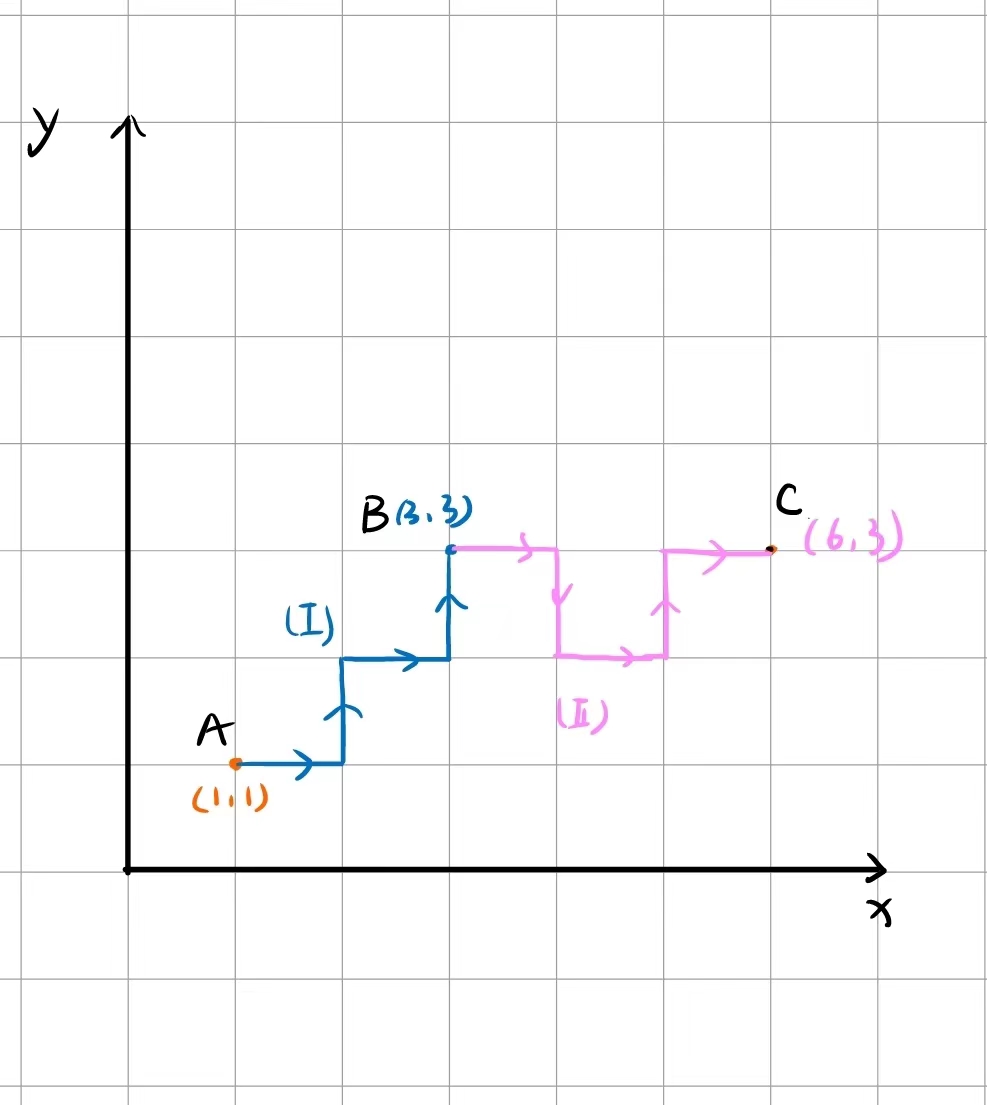
• 移动过程可以分为两个部分：
  • 未到达与C点横平或者竖直的时候：由于每走一步都要拐弯，所以可以等效为直接45°走。则走的步数就是B点的横/纵坐标-A点的横/纵坐标，求绝对值之和cnt。
  • 到达与C横平或竖直的B点之后： 分类讨论（举例抓出奇偶性规律）（假设水平/竖直差为d)
    • d为奇数：cnt+=2*d-1
    • d 为偶数：cnt+=2d

分类原因：见错误思路记录

code

#include <bits/stdc++.h>

typedef long long ll;

using namespace std;

struct Data

{

    int a;

    int b;

} dot1, dot2;

ll t1, t2, ans, d,first;

int main()

{

    cin >> dot1.a >> dot1.b >> dot2.a >> dot2.b;

    t1 = abs(dot1.a - dot2.a);

    t2 = abs(dot1.b - dot2.b);

    first = min(t1, t2);//横平竖直选一个短的走

    ans = first*2;

    d = max(t1, t2) - first;

    //假设平齐了，其实是要减去已经走了的横坐标，但是因为是45°所以直接减first

    if(d%2==0)

        ans += d * 2;

    else

        ans += d * 2 - 1;

    cout << ans << endl;

    return 0;

}

错误记录

本来采用了模拟的思路。第一步通过比较出发点和结束点的横纵坐标来确定。如果前一步是上下，则后一次是左右，具体左右根据所在点和结尾点的横坐标大小比较来确定。
这貌似没问题，当时也花了很多时间在找原因。其实从例图来看就知道，如果第一步走上，则不是最短的。走到B点会发现没法向右走。
即：当中途达到与结果点相平行或竖直的点处，如果间隔d是奇数，则下一步必须是朝着结果点方向的。而这就要求前一步必须与结果点方向垂直，不能是任意的。按原先的计算方式是可能实现不了这个特殊要求。

小结

• 模拟确实是解决很多题的一个方式，但是归纳数学式子往往是更多算法题的思路。
• 可以通过将过程分段，设置特殊节点的方式，然后人工走程序的逻辑，来查出错误。（因为分段了，所以点可以拉的远一点，也不怕乱）
• 另外，在写笔记的时候弄错了插入图片的相对路径表达。使用…/表示返回上一级目录。./表示同级目录。
• 特别鸣谢npy提供例图